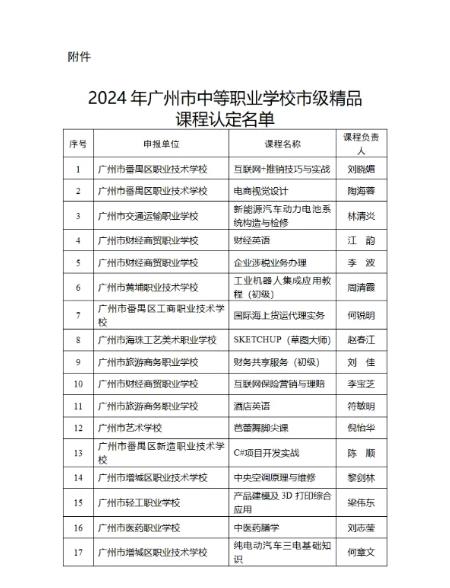
正弦函数单调递增区间
正弦函数的单调增区间:-(π/2)+2*k*π=x=(π/2)+2*k*π。
正弦函数的单调减区间:(π/2)+2*k*π=x=(3*π/2)+2*k*π。
正弦(sine),数学术语,在直角三角形中,任意一锐角∠A的对边与斜边的比叫做∠A的正弦,记作sinA(由英语sine一词简写得来),即sinA=∠A的对边/斜边。
扩展资料:
正弦函数的重要公式:
倍角半角公式:
1、sin(2α)=2*sin(α)*cos(α)。
2、sin(α/2)=±√((1-cosα ) /2)。
商的关系:
1、sinα/cosα=tanα=secα/cscα。
平方和关系:
1、(sinα)^2 +(cosα)^2=1。
正弦函数的导数公式:
1、(sinx)’=cosx。
在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆的直径,即a/sinA=b/sinB =c/sinC=2r=D(r为外接圆半径,D为直径)。
参考资料来源:百度百科-正弦


高一数学单调区间怎么求
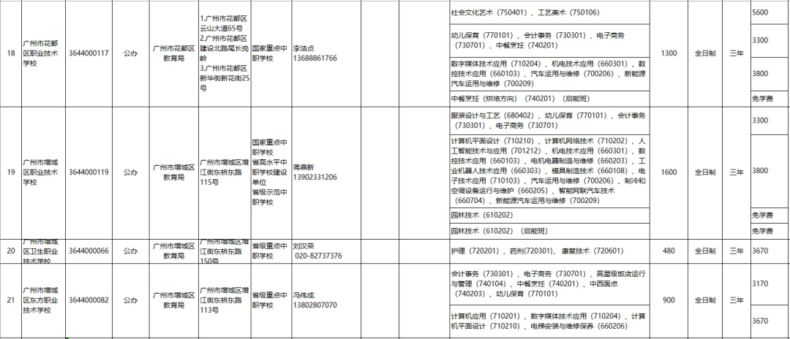
解不等式:
x²+4x-5≠0
得到:
x≠-5且x≠1
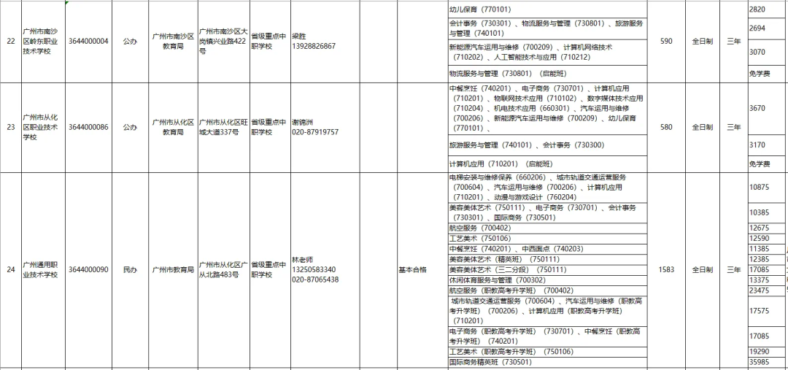
∴函数的定义域为
(-∞,-5)∪(-5,1)∪(1,+∞)
令g(x)=x²+4x-5
对称轴为x=-2,
当x<-2时,g(x)单调递减,
当x>-2时,g(x)单调递增。
根据复合函数的单调性,
原来函数的递增区间为
(-∞,-5)∪(-5,-2)
【即定义域内g(x)的单调递减区间】
cos函数的单调递增区间
cos的递增区间是[-π +2kπ,2kπ]或[π +2kπ,2π +2kπ]。
其他性质:
①周期性:最小正周期都是2π。
②奇偶性:偶函数。
③对称性:对称中心是(Kπ+π/2,0),K∈Z;对称轴是直线x=Kπ,K∈Z。
④单调性:在[2Kπ,2Kπ+π],K∈Z上单调递减;在[2Kπ+π,2Kπ+2π],K∈Z上单调递增。
定义域:R。
值域:[-1,1]。
最值:当X=2Kπ +π /2(K∈Z)时,Y取最大值1;当X=2Kπ +π (K∈Z时,Y取最小值-1。
余弦简介:
余弦(余弦函数),三角函数的一种。在Rt△ABC(直角三角形)中,∠C=90°(如概述图所示),∠A的余弦是它的邻边比三角形的斜边,即cosA=b/c,也可写为cosa=AC/AB。余弦函数:f(x)=cosx(x∈R)。
同角三角函数的基本关系式有:
倒数关系:tanα ·cotα=1、sinα ·cscα=1、cosα ·secα=1。
商的关系: sinα/cosα=tanα=secα/cscα、cosα/sinα=cotα=cscα/secα。
sin函数的单调区间公式
正弦函数的单调递减区间是(2kπ+π/2,2kπ+3π/2)(k∈n)。单调递增区间是(2kπ-π/2,2kπ+π/2)(k∈n)。
正弦函数的重要公式
倍角半角公式:
1、sin(2α)=2*sin(α)*cos(α)。
2、sin(α/2)=±√((1-cosα ) /2)。
商的关系:
sinα/cosα=tanα=secα/cscα。
平方和关系:
(sinα)^2 +(cosα)^2=1。
正弦函数余弦函数的单调区间
1、单调区间
正弦函数在[-π/2+2kπ,π/2+2kπ]上单调递增,在[π/2+2kπ,3π/2+2kπ]上单调递减
余弦函数在[-π+2kπ,2kπ]上单调递增,在[2kπ,π+2kπ]上单调递减
sin图像单调递增区间
y=sinx的单调区间如下:
单调增区间是[ -π/2+2kπ,π/2+2kπ] k∈Z。
单调减区间是[π/2+2kπ,3π/2+2kπ] k∈Z。
sinx的其他性质:
1、最值和零点:
①最大值:当x=2kπ+(π/2) ,k∈Z时,y(max)=1。
②最小值:当x=2kπ+(3π/2),k∈Z时,y(min)=-1。
零值点: (kπ,0) ,k∈Z。
2、对称性
对称轴:关于直线x=(π/2)+kπ,k∈Z对称。
中心对称:关于点(kπ,0),k∈Z对称。
3、周期性
最小正周期:2π。
奇偶性:奇函数 (其图象关于原点对称)。
sinx函数的相关简介:
sinx函数,即正弦函数,三角函数的一种。正弦函数是三角函数的一种。对于任意一个实数x都对应着唯一的角(弧度制中等于这个实数),而这个角又对应着唯一确定的正弦值sinx,这样,对于任意一个实数x都有唯一确定的值sinx与它对应,按照这个对应法则所建立的函数,表示为y=sinx,叫做正弦函数。




















 成立时间:1956年评级得分:93
成立时间:1956年评级得分:93



 成立时间:1984年
成立时间:1984年
 成立时间:1979年
成立时间:1979年

















 成立时间:1981年
成立时间:1981年



 成立时间:1965年
成立时间:1965年
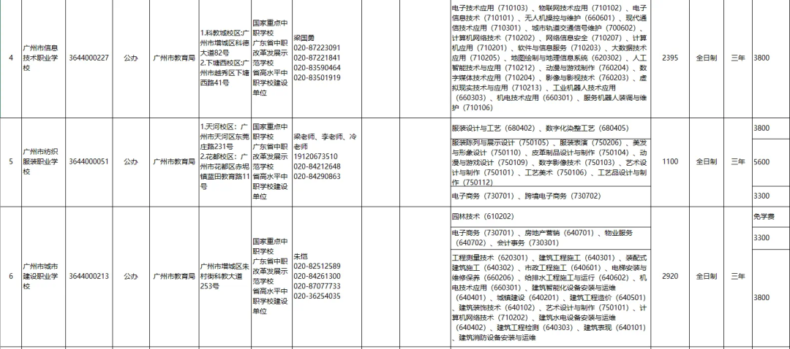
 1.广州市白云工商技师学院
优势:
智能制造专业突出,与广汽、腾讯等企业深度合作,学生未毕业即被预订,毕业生平均薪资达6800+元。
拥有“真枪实弹”的车间教室,连续8年位列广东技校榜首。
新增“数智营销技术”“商务数据分析”等前沿专业,适应数字经济需求。
2.广东省高级技工学校
优势:
政府重点支持,全省唯一副厅级技校,实验室设备先进(如元宇宙技术应用实验室)。
机电一体化、工业机器人等专业与制造业企业紧密对接,就业率常年保持在98%以上。
3.广东省轻工职业技术学校
优势:
轻工领域特色鲜明,食品加工、服装设计等专业实力强,教学设备先进。
与轻工行业企业合作,提供丰富实习机会,毕业生多进入食品、纺织行业。
4.广东省机械职业技术学校
优势:
机械制造与自动化领域的标杆学校,数控技术、模具设计专业省内领先。
实训基地配备库卡机械臂等先进设备,培养高精度技术人才。
5.深圳市高级技工学校
优势:
投资11亿建设实训基地,无人机实训直接使用大疆生产线,新能源汽修专业拆解特斯拉等高端车型。
新增智能网联汽车技术、人工智能等专业,贴合粤港澳大湾区产业需求。
6.广东省交通职业技术学校
优势:
交通运输类专业(如物流管理、汽车维修)就业率高,与广铁集团等企业合作定向培养。
新增“低空飞行器技术应用”“盾构机操作与维护”等特色交通专业。
7.广东省电子信息职业技术学校
优势:
电子信息与通信技术领域领先,计算机应用、电子技术应用专业实训设备完善。
与华为、中兴等企业合作开发课程,毕业生多进入通信和IT行业。
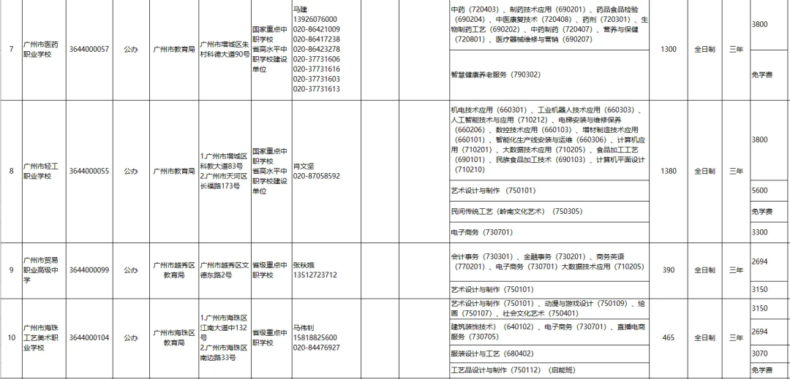
8.广东省医药职业技术学校
优势:
医药卫生类专业(药学、护理)就业率超95%,与广药集团合作订单培养。
拥有GMP标准药剂实训车间,实践教学资源丰富。
9.佛山市汽车工程学校
优势:
汽车检测与维修专业省内知名,配备智能汽车诊断设备和新能源车实训平台。
新增“车联网技术应用”专业,培养智能汽车领域人才。
10.广州市旅游商务职业学校
优势:
旅游管理、酒店管理专业实操性强,与高星级酒店合作,学生实习覆盖广交会等大型活动。
新增“智慧旅游服务”方向,结合数字化营销技能培养。
其他亮点学校
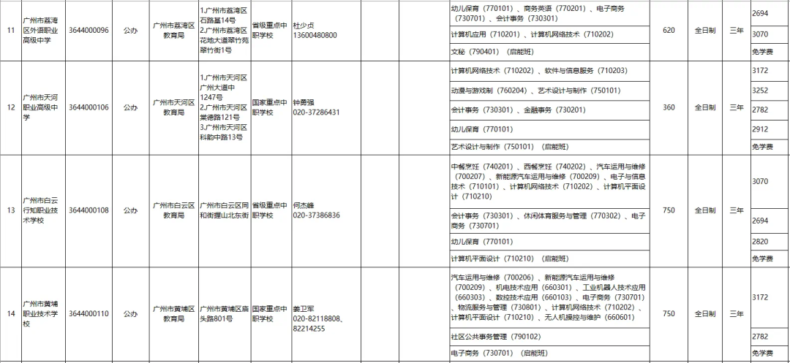
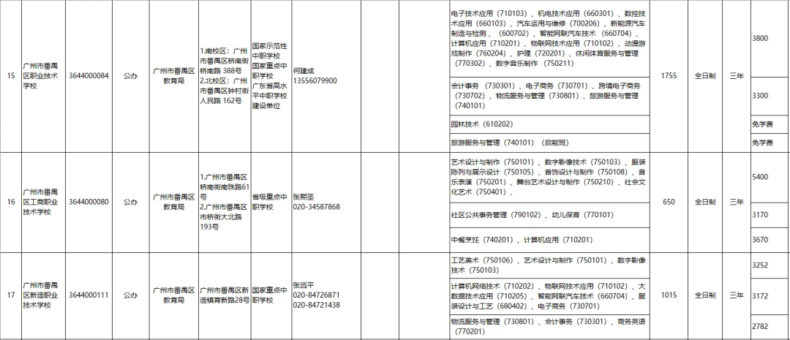
岭南工商第一高级技校:直播电商专业学生未毕业即成百万粉丝网红。
珠海市建筑工程学校:建筑类专业结合BIM技术教学,实训项目涵盖智慧城市管理。
选择建议
1.看专业匹配度:优先选择与产业需求契合的专业(如智能制造、新能源、电子信息)。
2.关注校企合作:合作企业直接影响实习和就业质量(如白云工商与腾讯、深圳技校与大疆)。
3.考察实训条件:先进设备(如工业机器人、元宇宙实验室)是技能培养的核心保障。
以上排名及信息综合自多个来源,具体选择需结合个人兴趣和职业规划。如需更多招生细节或专业对比,可参考各校官网或教育局
发布的最新数据。
1.广州市白云工商技师学院
优势:
智能制造专业突出,与广汽、腾讯等企业深度合作,学生未毕业即被预订,毕业生平均薪资达6800+元。
拥有“真枪实弹”的车间教室,连续8年位列广东技校榜首。
新增“数智营销技术”“商务数据分析”等前沿专业,适应数字经济需求。
2.广东省高级技工学校
优势:
政府重点支持,全省唯一副厅级技校,实验室设备先进(如元宇宙技术应用实验室)。
机电一体化、工业机器人等专业与制造业企业紧密对接,就业率常年保持在98%以上。
3.广东省轻工职业技术学校
优势:
轻工领域特色鲜明,食品加工、服装设计等专业实力强,教学设备先进。
与轻工行业企业合作,提供丰富实习机会,毕业生多进入食品、纺织行业。
4.广东省机械职业技术学校
优势:
机械制造与自动化领域的标杆学校,数控技术、模具设计专业省内领先。
实训基地配备库卡机械臂等先进设备,培养高精度技术人才。
5.深圳市高级技工学校
优势:
投资11亿建设实训基地,无人机实训直接使用大疆生产线,新能源汽修专业拆解特斯拉等高端车型。
新增智能网联汽车技术、人工智能等专业,贴合粤港澳大湾区产业需求。
6.广东省交通职业技术学校
优势:
交通运输类专业(如物流管理、汽车维修)就业率高,与广铁集团等企业合作定向培养。
新增“低空飞行器技术应用”“盾构机操作与维护”等特色交通专业。
7.广东省电子信息职业技术学校
优势:
电子信息与通信技术领域领先,计算机应用、电子技术应用专业实训设备完善。
与华为、中兴等企业合作开发课程,毕业生多进入通信和IT行业。
8.广东省医药职业技术学校
优势:
医药卫生类专业(药学、护理)就业率超95%,与广药集团合作订单培养。
拥有GMP标准药剂实训车间,实践教学资源丰富。
9.佛山市汽车工程学校
优势:
汽车检测与维修专业省内知名,配备智能汽车诊断设备和新能源车实训平台。
新增“车联网技术应用”专业,培养智能汽车领域人才。
10.广州市旅游商务职业学校
优势:
旅游管理、酒店管理专业实操性强,与高星级酒店合作,学生实习覆盖广交会等大型活动。
新增“智慧旅游服务”方向,结合数字化营销技能培养。
其他亮点学校
岭南工商第一高级技校:直播电商专业学生未毕业即成百万粉丝网红。
珠海市建筑工程学校:建筑类专业结合BIM技术教学,实训项目涵盖智慧城市管理。
选择建议
1.看专业匹配度:优先选择与产业需求契合的专业(如智能制造、新能源、电子信息)。
2.关注校企合作:合作企业直接影响实习和就业质量(如白云工商与腾讯、深圳技校与大疆)。
3.考察实训条件:先进设备(如工业机器人、元宇宙实验室)是技能培养的核心保障。
以上排名及信息综合自多个来源,具体选择需结合个人兴趣和职业规划。如需更多招生细节或专业对比,可参考各校官网或教育局
发布的最新数据。












 图片加载中…
图片加载中…


 图片加载中…
图片加载中…