波尔理论
1.玻尔理论
玻尔理论,关于原子结构的一种理论.1913年由玻尔提出.是在卢瑟福原子模型基础上加上普朗克的量子概念后建立的.要点是:
(1)原子核外的电子只能在某些规定的轨道上绕转,此时并不发光;
(2)电子从高能量的轨道跳到低能量的轨道时,原子发光.
具体来说,玻尔理论包括三条假说
1、原子能量的量子化假设:原子只能处于一系列不连续的能量状态中,在这些状态中的原子是稳定的,电子虽然做加速运动,但并不向外辐射能量.
2、原子能级的跃迁假设:原子从一个定态跃迁到另一个定态时,原子辐射一定频率的光子,光子的能量由这两种定态的能量差决定.
3、原子中电子运动轨道量子化假设:原子的不同能量状态对应于电子的不同运行轨道.由于原子的能量状态是不连续的,因此电子运动的轨道也可能是不连续的,即电子不能在任意半径的轨道上运动
玻尔理论的优点:
成功解释了氢原子光谱不连续的特点,解释了当时出现的”紫外灾难”.
玻尔理论的局限性
这个理论本身仍是以经典理论为基础,且其理论又与经典理论相抵触.它只能解释氢原子的光谱,在解决其他原子的光谱是就遇到了困难,如把理论用于非氢原子时,理论结果与实验不符,且不能求出谱线的强度及相邻谱先之间的宽度.这些缺陷主要是由于把微观粒子(电子,原子等)看作是经典力学中的质点,从而把经典力学规律强加于微观粒子上(如轨道概念)而导致的.
“玻尔理论”的提出,打破了经典物理学一统天下的局面,开创了揭示微观世界基本特征的前景,为量子理论体系奠定了基础,这是一种了不起的创举,不愧为爱因斯坦的评价--玻尔的电子壳层模型是思想领域中最高的音乐神韵.
2.解释其内容与应用:
卢瑟福的原子核式结构模型能成功地解释 粒子散射实验,但无法解释原子的稳定性和原子光谱是明线光谱等问题.为此,1913年玻尔提出了开创性的三个假设:
(1)定态假设:原子只能处于一系列不连续的能量的状态中,在这些状态中原子是稳定,电子虽然绕原子核做圆周运动,但并不向外辐射能量,这些状态叫定态.
(2)跃迁假设:电子从一个定态轨道跃迁到另一个定态轨道上时,会辐射或吸收一定频率的光子,能量由这两种定态的能量差来决定,即
(3)角动量量子化假设:电子绕核运动,其轨道半径不是任意的,只有电子的轨道角动量(轨道半径r和电子动量mv的乘积)满足下列条件的轨道才是可能的:
n=1,2,3……
式中的n是正整数,称为量子数.
4.玻尔理论在氢原子中的应用
(1)氢原子核外电子轨道的半径
设电子处于第n条轨道,轨道半径为r,根据玻尔理论的角动量量子化假设得
n=1,2,3…… (1)
电子绕原子核作圆周运动时,由电子和原子核之间的库仑力来提供向心力,所以有
(2)
由(1)(2)式可得
n=1,2,3……
当n=1时,第一条轨道的半径为
=5.3×10 –11m
其他可能的轨道半径为
,4r1 ,9r1 , 16r1 , 25r1 …
(2)氢原子的能级
当电子在第n条轨道上运动时,原子系统的总能量E叫做第n条轨道的能级,其数值等于电子绕核转动时的动能和电子与原子核的电势能的代数和
En = (3)
由(2)式得
(4)
将(4)式代入(3)式得
En = (5)
这就是氢原子的能级公式
当n=1时,第一条轨道的能级为
E1 = = —13.6eV
其他可能轨道的能级为
E n= = eV n=2,3,4……
由轨道的半径表达式可以看出,量子数n越大,轨道的半径越大,能级越高.n=1时能级最低,这时原子所处的状态称为基态,n=2,3,4,5……时原子所处的状态称为激发态.
(3)玻尔理论对氢光谱的解释
由玻尔理论可知,氢原子中的电子从较高能级(设其量子数为n)向较低能级(设其量子数为m)跃迁时,它向外辐射的光子能量为
=
辐射的光子频率为
=
将上式改写为
= =
将上式和里德伯公式做比较得
R= =1.097373×10 7 m –1
这个数据和实验所得的数据1.0967758×10 7m-1基本一致.因此用玻尔理论能较好地解释氢原子的光谱规律,包括氢光谱的各种线系.例如:赖曼系、巴尔末系、帕邢系、布喇开系等的规律.当然,玻尔理论也有局限性,它在解释两个以上电子的比较复杂的原子光谱时遇到困难.后来诞生了量子理论——量子力学,在量子力学中,玻尔理论中的电子轨道,只不过是电子出现机会最多的地方.
(四)原子的受激辐射——激光
原子辐射有两种情形:(1)自发辐射:处于激发态E2的原子,由于不稳定自发地跃迁到低能的E1上,同时辐射光子.光子的能量为 = ,普通的光源发光就属于这种辐射.它辐射的光子彼此能独立,发射的方向和初相位都不相同,所以我们可以从各个方向看到它发出的光.(2)受激辐射;当原子处于激发态E2时恰好有能量为 = 的光子趋近它,原子就可能受到此外来光子的激励而跃迁到低能态E1上,同时发射出一个和外来光子完全一样的光子.
激光就是由受激辐射产生的,一个入射光子由于引起受激辐射可以得到两个同样的光子,如果这两个光子在媒质中传播时再引起其他原子发生受激辐射,就会产生越来越多的相同的光子,使光得到加强,这就是激光,激光具有高单色性、高相干性、高亮度、而且方向性好.
二.原子核
(一)放射性元素的衰变
一些不稳定的原子核会自发地转变成另一种原子核同时放出射线,通常有 射线、 射线和 射线. 射线是氦原子核组成的粒子流, 射线是高速的电子流, 射线是波长很短的电磁波.原子核由于放出某种粒子而转变成新核的过程叫衰变.
原子核是一个量子体系,核衰变是原子核自发产生的变化,是一个量子跃迁的过程,它服从量子力学的统计规律.对任何一个放射性元素,它发生衰变的时刻是不可预告的,但对足够多的同一种放射性元素的集合,作为一个集体,它的衰变规律是则是十分精确的.用N0表示初始时的原子核数,经t时间后衰变的原子核数为N,则有
N = N0 (1)
这就是放射性衰变服从的指数衰减规律,式中 代表一个原子核在单位时间内发生衰变的几率,称为衰变常数.
放射性元素衰变有一定的速率,我们把放射性元素的原子核有半数发生衰变需要的时间叫半衰期T.即当t = T时,有 ,由(1)式可得
T=
或者写为
对某种确定的放射性元素,原子核发生衰变的时间有早也有晚,它们存在的时间不一样.理论上常用平均寿命 来表示放射性元素在衰变前的平均生存时间,放射性元素的平均寿命可表示为
原子核放出射线后自身就发生衰变,在衰变过程中,质量数、电荷数、能量、动能是守恒的.根据质量数和电荷数的守恒定律,可以判定衰变的产物;根据能量守恒定律,结合衰变前后粒子的质量,可以求出衰变过程中所放出的能量.
(二)原子核的结合能与质能方程
核子在结合成原子核时,由于有强大的核力作用,必须释放一定的能量.反之,将原子核分解成核子时,则要吸收同样多的能量,这个能量叫原子核的结合能.由于核子结合成原子核时放出了结合能,因此核的质量跟组成它的核子的质量比较起来就要小一些,设由Z个质子、N个中子组成的原子核,其质量为M,如果这Z个质子,N个中子是分散的,总质量应为Z m p + N m n,则由分散到结合在一起质量相差
这叫做原子核结合过程的质量亏损.
由爱因斯坦的相地论的质能方程有
E= m c2
这个方程表示物体的的能量增加 E,那么它的质量也相应地增加 ,反之亦然.式中c为真空中的光速.
所以在原子核结合过程中,质量亏损与能量变化的关系为
E= m c2
这就是原子核的结合能.原子核的结合能与其核子数之比叫每个核子的平均结合能.不同原子核的平均结合能不同,轻核和重核的平均结合能都较小,中等质量数的原子核,平均结合能较大,质量数为50—60的原子核平均结合能最大.
(三)核的裂变和聚变
1.重核的核子平均结合能比中等质量的核的核子平均结合能小,因此重核分裂成中等质量的核时,会有一部分原子核结合能释放出来,这种核反应叫裂变,如铀核裂变.当中子打击铀235后,应形成处于激发状态的复核,复核裂变为质量差不多相等的碎片,同时放出2—3个中子和原子核结合能
U+ n Xe + Sr + 2 n + 200Mev
这些中子如能再引起其它铀核裂变,就可使裂变反应不断地进行下去,这种反应叫链式反应,释放出大量的能量.原子弹、原子反应堆等装置就是利用U核裂变的原理制成的.链式反应要不断进行下去的一个重要条件是每个核裂变时产生的中子数要在一个以上.
2.轻的原子核变成较重的原子核时,也会释放出更多的原子核结合能,这种轻核结合成质量较大的核叫做聚变.如:
H+ H He + n + 17.6Mev
使核发生聚变,必须使它们接近到10-15米.一种办法是把核加热到很高温度,使核的热运动协能足够大,能够克服相互间的库仑斥力,在互相碰撞中接近到可以发生聚变的程度,因此,这种反应又叫做热核反应.氢弹是根据聚变的原理制成的.
玻尔理论公式
玻尔理论角动量公式:L=mvr。
角动量:
在这个旋转系统中,,公式的推理,存在类似的物理问题。在一个没有摩擦的封闭轨道上作旋转运动的系统中,一个不受外力矩作用的运动物体将一直保持角动量恒定的旋转运动状态不变。角动量的大小等于质量、速度和轨道半径的乘积,即:L=mvr.在玻尔模型中,如果一个电子从一个轨道跳到另一个轨道,其角动量的变化必须是h/2pai的整数倍。希望我的回答对你有帮助,欢迎采纳我的回答,谢谢。


玻尔的三个理论
波尔理论的三个假设有:① 原子系统只能存在于一系列不连续的能量状态中(E1、E2、E3···),在这些状态中,电子绕核作加速运动而不辐射能量,这种状态称这为原子系统的稳定状态(定态)②频率条件:当原子从一个定态跃迁到另一个定态时,发出或吸收单色辐射的频率满足:
只有当原子从一个较大的能量的稳定状态跃迁到另一较低能量的稳定状态时,才发射单色光,反之,当原子在较低能量的稳定状态时,吸收了一定光子能量就可跃迁到较大能量的稳定状态。③处于稳定态中,电子绕核运动的角动量满足角动量量子化条件
假设1 是经验性的,它解决了原子的稳定性问题;
假设2 是从普朗克量子假设引申来的,因此是合理的,它能解释线光谱的起源。
假设3 表述的角动量量子化原先是人为加进去的,后来知道它可以从德布罗意假设得出;
玻尔定律公式
一定质量的某种气体,
在温度不变的情况下,压强与体积成反比。
这个结论是英国科学家玻意耳(1627-1691)和法国科学家马略特(1620-1684)各自通过实验发现的,叫做玻意耳定律。
玻尔理论创始人
原子能量的量子化假设、原子能级的跃迁假设和原子中电子运动轨道量子化假设。
玻尔理论是关于原子结构的一种理论,1913年由玻尔提出,是在卢瑟福原子模型基础上加上普朗克的量子概念后建立的。玻尔理论包括三条假说,分别是原子能量的量子化假设、原子能级的跃迁假设和原子中电子运动轨道量子化假设。
玻尔理论的要点:原子核外的电子只能在某些规定的轨道上绕转,此时并不发光;电子从高能量的轨道跳到低能量的轨道时,原子发光。
意义
玻尔理论不但回答了氢原子稳定存在的原因,而且还成功地解释了氢原子和类氢原 子的光谱现象。氢原子在正常状态时,核外电子处于能量最低的基态,在该状态下运动的 电子既不吸收能量,也不放出能量,电子的能量不会减少,因而不会落到原子核上,原子不 会毁灭。
当氢原子从外界获得能量时,电子就会跃迁到能盘较高的激发态,处于激发态的 电子不稳定,就会自发地跃迁回能量较低的轨道,同时将能量以光的形式发射出来。




















 成立时间:1956年评级得分:93
成立时间:1956年评级得分:93



 成立时间:1984年
成立时间:1984年
 成立时间:1979年
成立时间:1979年

















 成立时间:1981年
成立时间:1981年



 成立时间:1965年
成立时间:1965年
 1.广州市白云工商技师学院
优势:
智能制造专业突出,与广汽、腾讯等企业深度合作,学生未毕业即被预订,毕业生平均薪资达6800+元。
拥有“真枪实弹”的车间教室,连续8年位列广东技校榜首。
新增“数智营销技术”“商务数据分析”等前沿专业,适应数字经济需求。
2.广东省高级技工学校
优势:
政府重点支持,全省唯一副厅级技校,实验室设备先进(如元宇宙技术应用实验室)。
机电一体化、工业机器人等专业与制造业企业紧密对接,就业率常年保持在98%以上。
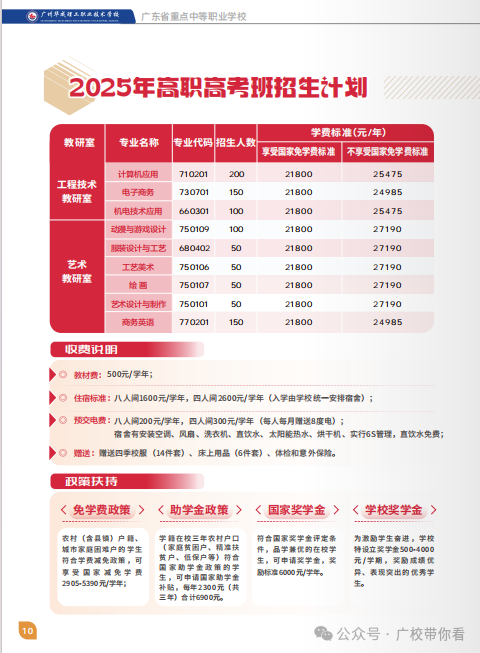
3.广东省轻工职业技术学校
优势:
轻工领域特色鲜明,食品加工、服装设计等专业实力强,教学设备先进。
与轻工行业企业合作,提供丰富实习机会,毕业生多进入食品、纺织行业。
4.广东省机械职业技术学校
优势:
机械制造与自动化领域的标杆学校,数控技术、模具设计专业省内领先。
实训基地配备库卡机械臂等先进设备,培养高精度技术人才。
5.深圳市高级技工学校
优势:
投资11亿建设实训基地,无人机实训直接使用大疆生产线,新能源汽修专业拆解特斯拉等高端车型。
新增智能网联汽车技术、人工智能等专业,贴合粤港澳大湾区产业需求。
6.广东省交通职业技术学校
优势:
交通运输类专业(如物流管理、汽车维修)就业率高,与广铁集团等企业合作定向培养。
新增“低空飞行器技术应用”“盾构机操作与维护”等特色交通专业。
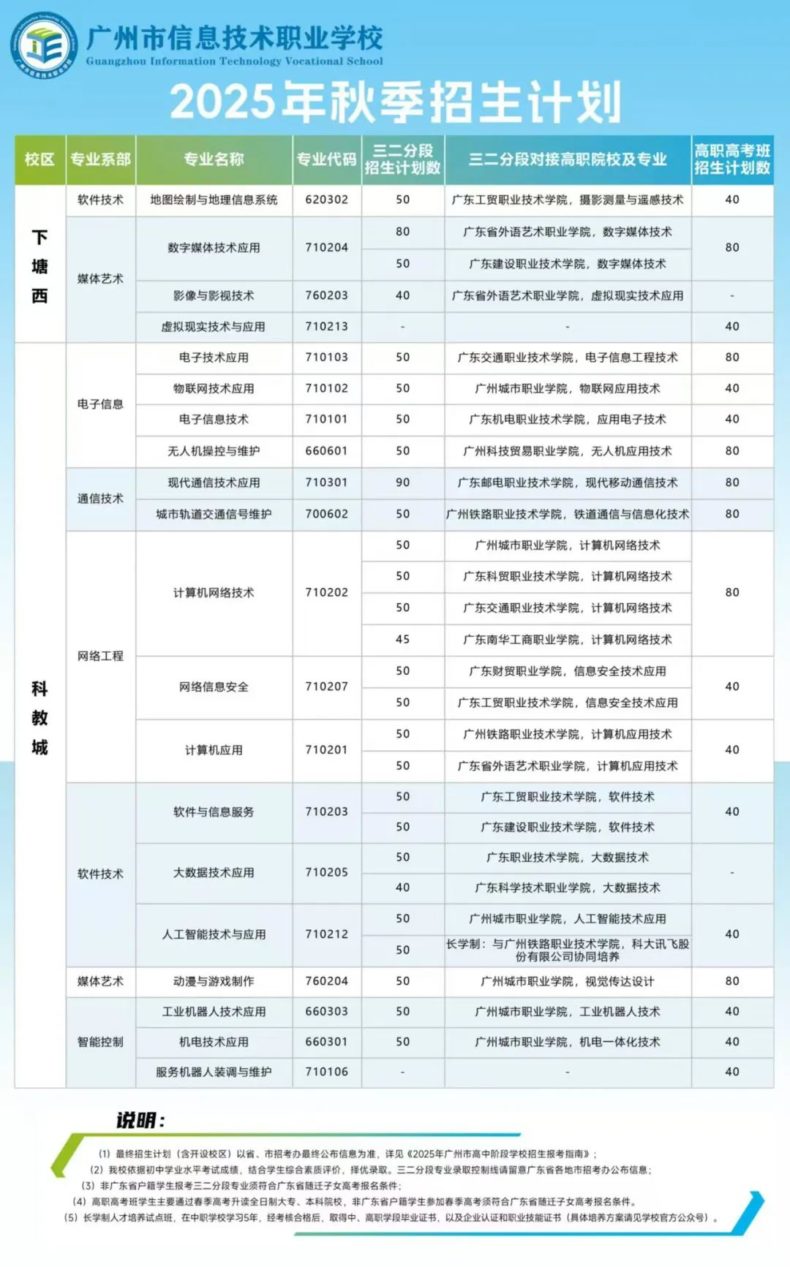
7.广东省电子信息职业技术学校
优势:
电子信息与通信技术领域领先,计算机应用、电子技术应用专业实训设备完善。
与华为、中兴等企业合作开发课程,毕业生多进入通信和IT行业。
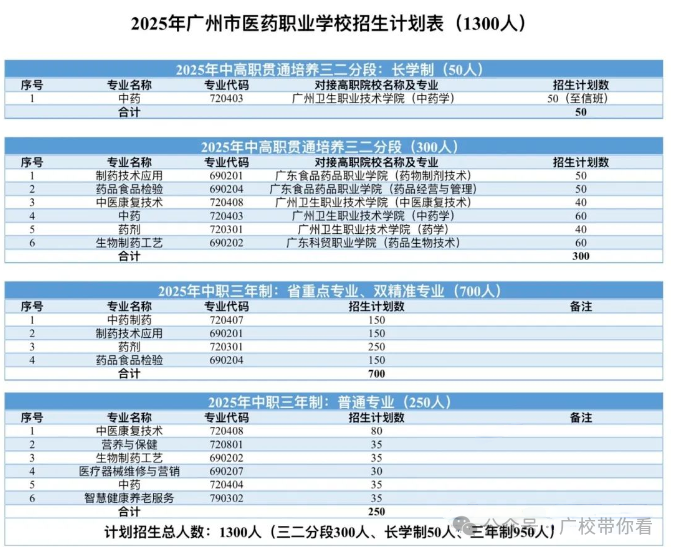
8.广东省医药职业技术学校
优势:
医药卫生类专业(药学、护理)就业率超95%,与广药集团合作订单培养。
拥有GMP标准药剂实训车间,实践教学资源丰富。
9.佛山市汽车工程学校
优势:
汽车检测与维修专业省内知名,配备智能汽车诊断设备和新能源车实训平台。
新增“车联网技术应用”专业,培养智能汽车领域人才。
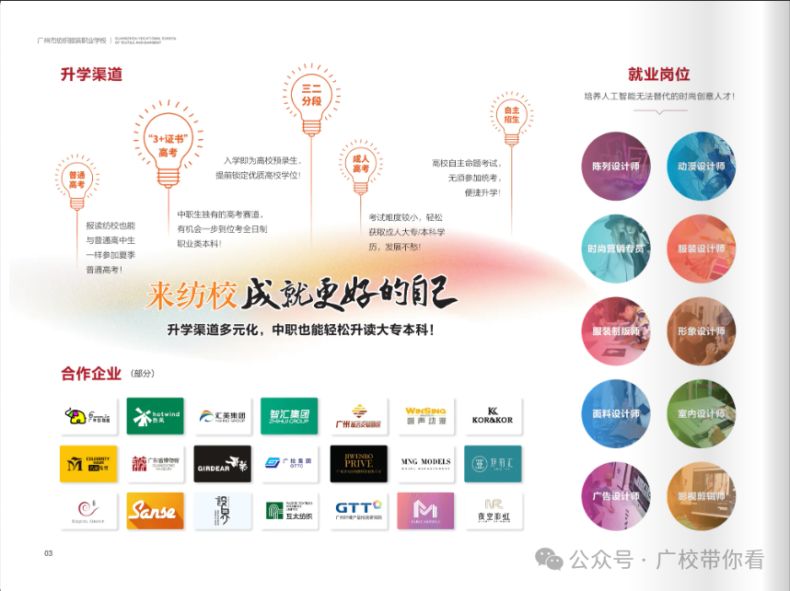
10.广州市旅游商务职业学校
优势:
旅游管理、酒店管理专业实操性强,与高星级酒店合作,学生实习覆盖广交会等大型活动。
新增“智慧旅游服务”方向,结合数字化营销技能培养。
其他亮点学校
岭南工商第一高级技校:直播电商专业学生未毕业即成百万粉丝网红。
珠海市建筑工程学校:建筑类专业结合BIM技术教学,实训项目涵盖智慧城市管理。
选择建议
1.看专业匹配度:优先选择与产业需求契合的专业(如智能制造、新能源、电子信息)。
2.关注校企合作:合作企业直接影响实习和就业质量(如白云工商与腾讯、深圳技校与大疆)。
3.考察实训条件:先进设备(如工业机器人、元宇宙实验室)是技能培养的核心保障。
以上排名及信息综合自多个来源,具体选择需结合个人兴趣和职业规划。如需更多招生细节或专业对比,可参考各校官网或教育局
发布的最新数据。
1.广州市白云工商技师学院
优势:
智能制造专业突出,与广汽、腾讯等企业深度合作,学生未毕业即被预订,毕业生平均薪资达6800+元。
拥有“真枪实弹”的车间教室,连续8年位列广东技校榜首。
新增“数智营销技术”“商务数据分析”等前沿专业,适应数字经济需求。
2.广东省高级技工学校
优势:
政府重点支持,全省唯一副厅级技校,实验室设备先进(如元宇宙技术应用实验室)。
机电一体化、工业机器人等专业与制造业企业紧密对接,就业率常年保持在98%以上。
3.广东省轻工职业技术学校
优势:
轻工领域特色鲜明,食品加工、服装设计等专业实力强,教学设备先进。
与轻工行业企业合作,提供丰富实习机会,毕业生多进入食品、纺织行业。
4.广东省机械职业技术学校
优势:
机械制造与自动化领域的标杆学校,数控技术、模具设计专业省内领先。
实训基地配备库卡机械臂等先进设备,培养高精度技术人才。
5.深圳市高级技工学校
优势:
投资11亿建设实训基地,无人机实训直接使用大疆生产线,新能源汽修专业拆解特斯拉等高端车型。
新增智能网联汽车技术、人工智能等专业,贴合粤港澳大湾区产业需求。
6.广东省交通职业技术学校
优势:
交通运输类专业(如物流管理、汽车维修)就业率高,与广铁集团等企业合作定向培养。
新增“低空飞行器技术应用”“盾构机操作与维护”等特色交通专业。
7.广东省电子信息职业技术学校
优势:
电子信息与通信技术领域领先,计算机应用、电子技术应用专业实训设备完善。
与华为、中兴等企业合作开发课程,毕业生多进入通信和IT行业。
8.广东省医药职业技术学校
优势:
医药卫生类专业(药学、护理)就业率超95%,与广药集团合作订单培养。
拥有GMP标准药剂实训车间,实践教学资源丰富。
9.佛山市汽车工程学校
优势:
汽车检测与维修专业省内知名,配备智能汽车诊断设备和新能源车实训平台。
新增“车联网技术应用”专业,培养智能汽车领域人才。
10.广州市旅游商务职业学校
优势:
旅游管理、酒店管理专业实操性强,与高星级酒店合作,学生实习覆盖广交会等大型活动。
新增“智慧旅游服务”方向,结合数字化营销技能培养。
其他亮点学校
岭南工商第一高级技校:直播电商专业学生未毕业即成百万粉丝网红。
珠海市建筑工程学校:建筑类专业结合BIM技术教学,实训项目涵盖智慧城市管理。
选择建议
1.看专业匹配度:优先选择与产业需求契合的专业(如智能制造、新能源、电子信息)。
2.关注校企合作:合作企业直接影响实习和就业质量(如白云工商与腾讯、深圳技校与大疆)。
3.考察实训条件:先进设备(如工业机器人、元宇宙实验室)是技能培养的核心保障。
以上排名及信息综合自多个来源,具体选择需结合个人兴趣和职业规划。如需更多招生细节或专业对比,可参考各校官网或教育局
发布的最新数据。












 图片加载中…
图片加载中…


 图片加载中…
图片加载中…